Checked out and looked at several articles relating antennas in this Great Site
www.antennex.com

TRANSMISSION LINE AND ANTENNA

TRANSMISSION LINE FORMULAS

The characteristic impedance of a transmission line is defined as the input impedance of a line of the same configuration and dimensions but of infinite length. When a line of finite length is terminated with an impedance equal to its own characteristic impedance, the line is said to be matched.

Coaxial Line

The characteristic impedance of a coaxial line (Fig. 1) is given by:

FIG 1

where,

    4 is the characteristic impedance,
    D is the inside diameter of the outer conductor,
    d is the outside diameter of the inner conductor expressed in the same units as D,
    kisthedielectricconstantof theinsulating material* (k equals 1 for dry air).
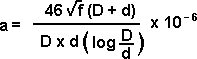The attenuation of coaxial fine in decibels per foot can be determined by the formula:

where,

    a is the attenuation in decibels per foot of line,
    f is the frequency in megahertz,
    D is the inside diameter of lhe outer conductor in inches,
    d is the outside diameter of the inner conductor in inches.

Parallel-Conductor Line

The characteristic impedance of parallel-conductor line (twin-lead) as shown in Fig. 2 is determined by the formula:

FIG. 2

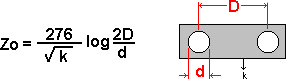
where,

    Z,, is the characteristic impedance,
    D is the center-to-center distance between conductors,
    d is the diameter of the conductors in the same units as D,
    k is the dielectric constant of the insulating material between conductors* (k equals 1 for dry air).
* For a list of dielectric constants of materials, see Table 2-1. Constants and Standards

ANTENNA

RF Current and Voltage distribution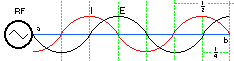

If a RF source is applied to a random length a - b wire then, the current distribution at the open end b will be always low and the voltage will be always high. As seen in the above graph the RF Current and Voltage distribution is divided in the wire appropriate with the physical ½ wavelength intervals

Radiating resistor

Vertical antenna

Rs = radiating resistor
dl = antenna length
l = wavelength

Short antenna

compared to wavelength

Rs = radiating resistor
heff = antenna effective length
l = wavelength

ANTENNA IMPEDANCE

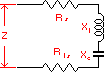
Antenna equivalent circuit

Z = Rs + Rls + Sx

where
    Z = Antenna Impedance
    Rs = Radiating Resistance
    Rls = Resistive losses(dielectric,
            absorbsion, ground, etc)
    Sx = Xc + XL
Updated February 1999